|
|
 |
| Planimetria |
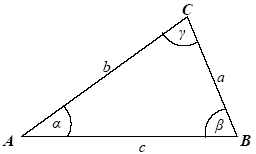
a,b,c - długości boków, leżących odpowiednio naprzeciwko wierzchołków
2p=a+b+c - obwód trójkąta
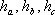 wysokości opuszczone na odpowiednie boki
R,r - promienie okręgów opisanego i wpisanego
Wzory na pole trójkąta
Twierdzenie sinusów
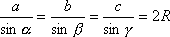
Twierdzenie cosinusów
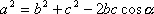
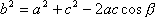
Związki miarowe w trójkącie prostokątnym
Załóżmy że kąt y jest prosty. Wówczas:
Twierdzenie Talesa (wraz z twierdzeniem odwrotnym do niego)
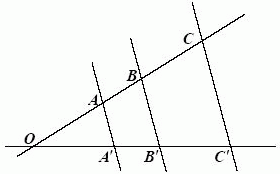
Proste AA', BB', CC' są parami równoległe wtedy i tylko wtedy, gdy zachodzi równość:
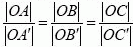
Czworokąty
Czworokąt, który ma co najmniej jedną parę boków równoległych.
Wzór na pole trapezu:
Równoległobok
Czworokąt, który ma dwie pary boków równoległych.
Wzory na pole równoległoboku:
Romb
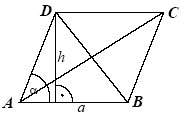
Czworokąt, który ma dwie pary boków równoległych jednakowej długości.
Wzory na pole rombu:
Deltoid
Czworokąt, który ma oś symetrii, zawierającą jedną z przekątnych.
Wzór na pole deltoidu:
Koło
Wzór na pole koła o promieniu r:
Obwód koła o promieniu r:
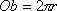
Wycinek koła
Wzór na pole wycinka koła o promieniu r i kącie środkowym alfa:
Długość łuku wycinka koła o promieniu r i kącie środkowym alfa :
Kąty w okręgu
Miara kąta wpisanego w okrąg jest równa połowie miary kąta środkowego, opartego na tym samym łuku.
Miary kątów wpisanych w okrąg, opartych na tych samych łukach są równe.
Okrąg opisany na czworokącie
Na czworokącie można opisać okrąg wtedy i tylko wtedy, gdy sumy miar jego przeciwległych kątów wewnętrznych są równe 180':
Okrąg wpisany w czworokąt
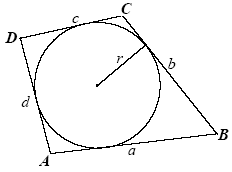
W czworokąt wypukły można wpisać okrąg wtedy i tylko wtedy, gdy sumy długości jego przeciwległych boków są równe:
|
|
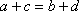